अध्याय 03 आंकड़ों का चित्रात्मक निरूपण
आपने विभिन्न प्रकार के आँकड़ों को दर्शाने वाले ग्राफ़, आरेख और नक्शे जरूर देखे होंगे। उदाहरण के लिए, कक्षा XI की पुस्तक Practical Work in Geography, Part-I (NCERT, 2006) के अध्याय 1 में दिखाए गए थीमैटिक नक्शे महाराष्ट्र के नागपुर जिले की राहत और ढाल, जलवायु परिस्थितियाँ, चट्टानों और खनिजों का वितरण, मिट्टियाँ, जनसंख्या, उद्योग, सामान्य भूमि उपयोग और फसल पैटर्न को दर्शाते हैं। इन नक्शों को संबंधित बड़ी मात्रा में आँकड़ों को एकत्र कर, संकलित कर और संसाधित करके बनाया गया है। क्या आपने कभी सोचा है कि यही जानकारी यदि सारणीबद्ध रूप में या वर्णनात्मक पाठ में होती तो क्या होता? शायद ऐसे संचार माध्यम से वे दृश्य प्रभाव नहीं बनाए जा सकते जो हम इन नक्शों के माध्यम से प्राप्त करते हैं। इसके अतिरिक्त, गैर-ग्राफ़ीय रूप में प्रस्तुत किसी भी जानकारी के बारे में निष्कर्ष निकालना समय लेने वाला कार्य भी होता। इसलिए, ग्राफ़, आरेख और नक्शे हमारी क्षमताओं को बढ़ाते हैं जिससे हम प्रस्तुत घटनाओं की सार्थक तुलना कर सकें, हमारा समय बचाते हैं और प्रस्तुत विशेषताओं का सरलीकृत दृश्य प्रस्तुत करते हैं। वर्तमान अध्याय में हम विभिन्न प्रकार के ग्राफ़, आरेख और नक्शे बनाने की विधियों पर चर्चा करेंगे।
आँकड़ों का निरूपण
आंकड़े उन घटनाओं के गुणों का वर्णन करते हैं जिनका वे प्रतिनिधित्व करते हैं। इन्हें विभिन्न स्रोतों से एकत्र किया जाता है (अध्याय 1)। भूगोलवेत्ता, अर्थशास्त्री, संसाधन वैज्ञानिक और निर्णय निर्माता आजकल बहुत सारे आंकड़ों का उपयोग करते हैं। सारणीबद्ध रूप के अतिरिक्त, आंकड़ों को किसी ग्राफिक या आरेखीय रूप में भी प्रस्तुत किया जा सकता है। ग्राफ, आरेख, मानचित्र और चार्ट जैसी दृश्य विधियों के माध्यम से आंकड़ों के रूपांतरण को आंकड़ों का प्रतिनिधित्व कहा जाता है। आंकड़ों की ऐसी प्रस्तुति किसी भौगोलिक क्षेत्र के भीतर जनसंख्या वृद्धि, वितरण और घनत्व, लिंग अनुपात, आयु-लिंग संरचना, व्यावसायिक संरचना आदि के प्रतिरूपों को समझना आसान बना देती है। एक चीनी कहावत है कि ‘एक चित्र हजारों शब्दों के समतुल्य है’। इसलिए, आंकड़ों के प्रतिनिधित्व की ग्राफिक विधि हमारी समझ को बढ़ाती है और तुलनाओं को आसान बनाती है। इसके अतिरिक्त, ऐसी विधियाँ मन पर अधिक समय तक छाप छोड़ती हैं।
ग्राफ, आरेख और मानचित्र बनाने के सामान्य नियम
1. उपयुक्त विधि का चयन
डेटा विभिन्न विषयों जैसे तापमान, वर्षा, जनसंख्या की वृद्धि और वितरण, विभिन्न वस्तुओं का उत्पादन, वितरण और व्यापार आदि को दर्शाते हैं। इन डेटा की विशेषताओं को एक उपयुक्त ग्राफ़िकल विधि द्वारा उपयुक्त रूप से दर्शाया जाना चाहिए। उदाहरण के लिए, तापमान या विभिन्न देशों/राज्यों के बीच विभिन्न समय अवधियों में जनसंख्या की वृद्धि से संबंधित डेटा को लाइन ग्राफ़ का उपयोग करके सबसे अच्छी तरह दर्शाया जा सकता है। इसी प्रकार, वर्षा या वस्तुओं के उत्पादन को दिखाने के लिए बार आरेख सबसे उपयुक्त हैं। जनसंख्या वितरण, मानव और पशु दोनों, या फसल उत्पादन क्षेत्रों के वितरण को डॉट मानचित्रों पर और जनसंख्या घनत्व को कोरोप्लेथ मानचित्रों का उपयोग करके उपयुक्त रूप से दर्शाया जा सकता है।
2. उपयुक्त स्केल का चयन
स्केल को डेटा के प्रतिनिधित्व के माप के रूप में आरेखों और मानचित्रों पर उपयोग किया जाता है। इसलिए, दिए गए डेटा सेटों के लिए उपयुक्त स्केल का चयन सावधानीपूर्वक किया जाना चाहिए और इसमें संपूर्ण डेटा को ध्यान में रखा जाना चाहिए जिसे दर्शाया जाना है। स्केल न तो बहुत बड़ा होना चाहिए और न ही बहुत छोटा।
3. डिज़ाइन
हम जानते हैं कि डिज़ाइन एक महत्वपूर्ण कार्टोग्राफिक कार्य है (देखें ‘Essentials of Map Making’ जैसा कि प्रैक्टिकल वर्क इन जियोग्राफी, पार्ट-आई (NCERT, 2006), कक्षा XI की पाठ्यपुस्तक के अध्याय 1 में चर्चा की गई है)। कार्टोग्राफिक डिज़ाइन के निम्नलिखित घटक महत्वपूर्ण हैं। इसलिए, इन्हें अंतिम आरेख/मानचित्र पर सावधानीपूर्वक दर्शाया जाना चाहिए।
शीर्षक
आरेख/नक्शे के शीर्षक में क्षेत्र का नाम, प्रयोग किए गए आंकड़ों का संदर्भ वर्ष और आरेख की उपशीर्षक इत्यादि शामिल होते हैं। इन घटकों को विभिन्न फ़ॉन्ट आकारों और मोटाई के अक्षरों और संख्याओं द्वारा दर्शाया जाता है। इसके अतिरिक्त, इनकी स्थिति भी महत्वपूर्ण होती है। सामान्यतः, शीर्षक, उपशीर्षक और संबंधित वर्ष को नक्शे/आरेख के शीर्ष के मध्य में दिखाया जाता है।
लीजेंड
लीजेंड या सूचकांक किसी भी आरेख/नक्शे का एक महत्वपूर्ण घटक होता है। यह नक्शे और आरेख में प्रयोग किए गए रंगों, छायांकन, प्रतीकों और चिन्हों की व्याख्या करता है। इसे सावधानीपूर्वक बनाया जाना चाहिए और नक्शे/आरेख की सामग्री से मेल खाना चाहिए। इसके अतिरिक्त, इसे उचित स्थान पर भी रखना होता है। सामान्यतः, लीजेंड को नक्शे की शीट के निचले बाएँ या निचले दाएँ भाग में दिखाया जाता है।
दिशा
नक्शे, पृथ्वी की सतह के एक भाग के प्रतिरूप होने के नाते, दिशाओं के अनुरूप उन्मुख होने चाहिए। इसलिए, दिशा चिह्न, अर्थात् उत्तर, को भी अंकित किया जाना चाहिए और अंतिम नक्शे पर उचित स्थान पर रखा जाना चाहिए।
आरेखों की रचना
आंकड़ों में मापने योग्य विशेषताएँ जैसे लंबाई, चौड़ाई और आयतन होते हैं। इन आंकड़ा-संबंधी विशेषताओं को दर्शाने के लिए बनाए गए आरेखों और नक्शों को निम्नलिखित प्रकारों में वर्गीकृत किया जा सकता है:
(i) एक-आयामी आरेख, जैसे रेखा ग्राफ, पॉली ग्राफ, बार आरेख, हिस्टोग्राम, आयु, लिंग, पिरामिड आदि;
(ii) दो-आयामी आरेख, जैसे पाई आरेख और आयताकार आरेख;
(iii) तीन-आयामी आरेख, जैसे घन और गोलाकार आरेख।
इन सभी प्रकारों के आरेखों और मानचित्रों की निर्माण विधियों पर चर्चा करना समय की कमी के कारण संभव नहीं होगा। इसलिए, हम सबसे अधिक बनाए जाने वाले आरेखों और मानचित्रों तथा उनके निर्माण की विधि का वर्णन करेंगे। ये हैं:
- रेखा आरेख
- पाई आरेख
- दंड आरेख
- वाइंड रोज़ और स्टार आरेख
- प्रवाह चार्ट
रेखा आरेख
रेखा आरेख सामान्यतः तापमान, वर्षा, जनसंख्या वृद्धि, जन्म दर और मृत्यु दर से संबंधित समय श्रेणी के आँकड़ों को दर्शाने के लिए बनाए जाते हैं। तालिका 3.1 उस आँकड़े को प्रदान करती है जिसका उपयोग चित्र 3.2 के निर्माण के लिए किया गया है।
रेखा आरेख का निर्माण
(a) आँकड़ों को गोल संख्याओं में बदलकर सरल बनाएँ, जैसे तालिका 3.1 में दर्शाए अनुसार वर्ष 1961 और 1981 की जनसंख्या वृद्धि दर को क्रमशः 2.0 और 2.2 के रूप में पूर्णांकित किया जा सकता है।
(b) $\mathrm{X}$ और $\mathrm{Y}$-अक्ष खींचें। समय श्रेणी के चर (वर्ष/महीने) को $\mathrm{X}$ अक्ष पर और आलेखित किए जाने वाले आँकड़े की मात्रा/मान (जनसंख्या वृद्धि प्रतिशत में या तापमान ${ }^{\circ}\mathrm{C}$ में) को $\mathrm{Y}$ अक्ष पर अंकित करें।
(c) उपयुक्त मापदंड चुनें और उसे Y-अक्ष पर लेबल करें। यदि आँकड़ों में ऋणात्मक संख्या शामिल हो, तो चयनित मापदंड उसे भी दर्शाए जैसा कि चित्र 3.1 में दिखाया गया है।

चित्र 3.1; रेखा ग्राफ का निर्माण
(द) चयनित पैमाने के अनुसार Y-अक्ष पर वर्ष/माह-वार मानों को दर्शाने के लिए आँकड़ों को प्लॉट करें, प्लॉट किए गए मानों के स्थान को एक बिंदु द्वारा चिह्नित करें और इन बिंदुओं को हाथ से खींची गई रेखा द्वारा जोड़ें।
उदाहरण 3.1: तालिका 3.1 में दिए गए आँकड़ों को दर्शाने के लिए एक रेखा ग्राफ का निर्माण करें:
तालिका 3.1; भारत में जनसंख्या की वृद्धि दर - 1901 से 2011
| वर्ष | वृद्धि दर प्रतिशत में |
|---|---|
| 1901 | - |
| 1911 | 0.56 |
| 1921 | -0.30 |
| 1931 | 1.04 |
| 1941 | 1.33 |
| 1951 | 1.25 |
| 1961 | 1.96 |
| 1971 | 2.20 |
| 1981 | 2.22 |
| 1991 | 2.14 |
| 2001 | 1.93 |
| 2011 | 1.79 |

चित्र 3.2; भारत में जनसंख्या की वार्षिक वृद्धि 1901-2011
गतिविधि
1911 और 1921 के बीच जनसंख्या में आए अचानक परिवर्तन के कारणों का पता लगाएं जैसा कि चित्र 3.2 में दिखाया गया है।
पॉलीग्राफ
पॉलिग्राफ एक रेखा ग्राफ है जिसमें दो या दो से अधिक चरों को समान संख्या में रेखाओं द्वारा तुरंत तुलना के लिए दर्शाया जाता है, जैसे कि विभिन्न फसलों जैसे चावल, गेहूं, दालों की वृद्धि दर या जन्म दर, मृत्यु दर और जीवन प्रत्याशा या विभिन्न राज्यों या देशों में लिंग अनुपात। विभिन्न चरों के मानों को दर्शाने के लिए विभिन्न रेखा पैटर्न जैसे सीधी रेखा ( _ _ ), टूटी रेखा (- – ), बिंद्दित रेखा (…..) या बिंद्दित और टूटी रेखा का संयोजन (-…-) या विभिन्न रंगों की रेखाओं का उपयोग किया जा सकता है (चित्र 3.3)।
उदाहरण 3.2: तालिका 3.2 में दिए गए विभिन्न राज्यों में लिंग अनुपात की वृद्धि की तुलना के लिए एक पॉलिग्राफ बनाइए:
**तालिका 3.2; चयनित राज्यों का लिंग अनुपात (1000 पुरुषों प्रति महिलाएं) - 1961-2011 **
| राज्य/केंद्र शासित प्रदेश | 1961 | 1971 | 1981 | 1991 | 2001 | 2011 |
|---|---|---|---|---|---|---|
| दिल्ली | 785 | 801 | 808 | 827 | 821 | 866 |
| हरियाणा | 868 | 867 | 870 | 860 | 846 | 877 |
| उत्तर प्रदेश | 907 | 876 | 882 | 876 | 898 | 908 |
स्रोत: जनगणना, 2011

चित्र. 3.3; चयनित राज्यों का लिंग अनुपात 1961-2011
दंड आरेख
दंड आरेख समान चौड़ाई के स्तंभों के माध्यम से खींचे जाते हैं। इसे स्तंभीय आरेख भी कहा जाता है। दंड आरेख बनाते समय निम्नलिखित नियमों का पालन किया जाना चाहिए:
(क) सभी पट्टियों या स्तंभों की चौड़ाई समान होनी चाहिए।
(ख) सभी पट्टियों को समान अंतराल/दूरी पर रखा जाना चाहिए।
(ग) पट्टियों को अलग और आकर्षक बनाने के लिए उन्हें रंगों या पैटर्न के साथ छायांकित किया जा सकता है।
सरल, संयुक्त या बहुपट्टी आरेख को आंकड़ों की विशेषताओं के अनुरूप बनाया जा सकता है।
सरल पट्टी आरेख
एक सरल पट्टी आरेख तत्काल तुलना के लिए बनाया जाता है। यह सलाह दी जाती है कि दिए गए आंकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करें और आंकड़ा चरों को तदनुसार प्लॉट करें। हालांकि, समय श्रृंखला आंकड़ों को समय अवधि के क्रम के अनुसार प्रस्तुत किया जाता है।
उदाहरण 3.3: तिरुवनंतपुरम की वर्षा आंकड़ों को सरल पट्टी आरेख के रूप में प्रस्तुत करें जैसा कि तालिका 3.3 में दिया गया है:
तालिका 3.3; तिरुवनंतपुरम की औसत मासिक वर्षा
| महीने | ज | फ | म | अ | मा | जू | जु | आ | स | ओ | न | द |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| वर्षा सेमी में | 2.3 | 2.1 | 3.7 | 10.6 | 20.8 | 35.6 | 22.3 | 14.6 | 13.8 | 27.3 | 20.6 | 7.5 |
निर्माण
ग्राफ पेपर पर $X$ और Y-अक्ष खींचें। Y-अक्ष पर $5 \mathrm{~cm}$ का अंतराल लें और वर्षा आंकड़ों को $\mathrm{cm}$ में प्लॉट करने के लिए उसे चिह्नित करें। $\mathrm{X}$-अक्ष को 12 समान भागों में विभाजित करें ताकि 12 महीनों को दर्शाया जा सके। प्रत्येक महीने के लिए वास्तविक वर्षा मानों को चयनित स्केल के अनुसार प्लॉट किया जाएगा जैसा कि चित्र 3.4 में दिखाया गया है।

चित्र 3.4; तिरुवनंतपुरम की औसत मासिक वर्षा
रेखा और दंड आलेख
रेखा और दंड आलेखों को अलग-अलग बनाने के बाद इन्हें संयुक्त रूप से भी चित्रित किया जा सकता है ताकि कुछ निकटतम संबंधित विशेषताओं, जैसे मासिक औसत तापमान और वर्षा के जलवायु-आंकड़ों, को दर्शाया जा सके। ऐसा करते समय एक ही आरेख बनाया जाता है जिसमें X-अक्ष पर माह दर्शाए जाते हैं जबकि तापमान और वर्षा के आंकड़े आरेख के दोनों ओर Y-अक्ष पर दिखाए जाते हैं।
उदाहरण 3.4: तालिका 3.4 में दिए गए दिल्ली के औसत मासिक वर्षा और तापमान आंकड़ों को रेखा आलेख और दंड आरेख द्वारा दर्शाइए:
तालिका 3.4; दिल्ली में औसत मासिक तापमान और वर्षा
| माह | तापमान ${ }^{\circ}\mathrm{C}$ में | वर्षा सेमी में |
|---|---|---|
| जन. | 14.4 | 2.5 |
| फर. | 16.7 | 1.5 |
| मार्च | 23.30 | 1.3 |
| अप्रैल | 30.0 | 1.0 |
| मई | 33.3 | 1.8 |
| जून | 33.3 | 7.4 |
| जुलाई | 30.0 | 19.3 |
| अगस्त | 29.4 | 17.8 |
| सित. | 28.9 | 11.9 |
| अक्तू. | 25.6 | 1.3 |
| नव. | 19.4 | 0.2 |
| दिस. | 15.6 | 1.0 |
निर्माण
(a) उपयुक्त लंबाई के $\mathrm{X}$ और $\mathrm{Y}$-अक्ष खींचें और $\mathrm{X}$-अक्ष को 12 भागों में बांटकर वर्ष के माह दर्शाएं।
(b) तापमान डेटा के लिए Y-अक्ष पर 5°C या 10°C के समान अंतराल वाली उपयुक्त स्केल चुनें और उसे दाईं ओर लेबल करें।
(c) इसी प्रकार, वर्षा डेटा के लिए Y-अक्ष पर 5 cm या 10 cm के समान अंतराल वाली उपयुक्त स्केल चुनें और उसे बाईं ओर लेबल करें।
(d) तापमान डेटा को रेखा ग्राफ से और वर्षा को बार आरेख से चित्रित करें जैसा कि Fig. 3.5 में दिखाया गया है।

Fig. 3.5; दिल्ली में तापमान और वर्षा
बहु-बार आरेख
बहु-बार आरेख दो या दो से अधिक चरों की तुलना के उद्देश्य से बनाए जाते हैं। उदाहरण के लिए, एक बहु-बार आरेख यह दिखाने के लिए बनाया जा सकता है कि कुल, ग्रामीण और शहरी जनसंख्या में पुरुषों और महिलाओं का अनुपात क्या है या विभिन्न राज्यों में सिंचित क्षेत्र के कुल क्षेत्रफल में नहर, नलकूप और कुएँ की सिंचाई का हिस्सा कितना है।
उदाहरण 3.5: तालिका 3.5 में दिए गए अनुसार भारत में 1951-2011 के दौरान दशकीय साक्षरता दर को दिखाने के लिए उपयुक्त बार आरेख बनाएं:
निर्माण
(a) उपरोक्त डेटा को दर्शाने के लिए बहु-बार आरेख चुना जा सकता है।
(b) चुनी गई स्केल के अनुसार X-अक्ष पर समय श्रेणी डेटा और Y-अक्ष पर साक्षरता दर अंकित करें। तालिका 3.5; भारत में साक्षरता दर, 1951-2011 (प्रतिशत में)
तालिका 3.5; भारत में साक्षरता दर, 1951–2011 (प्रतिशत में)
| वर्ष | $\hspace{1cm}$ साक्षरता दर | ||
|---|---|---|---|
| कुल जनसंख्या |
पुरुष | महिला | |
| 1951 | 18.33 | 27.16 | 8.86 |
| 1961 | 28.3 | 40.4 | 15.35 |
| 1971 | 34.45 | 45.96 | 21.97 |
| 1981 | 43.57 | 56.38 | 29.76 |
| 1991 | 52.21 | 64.13 | 39.29 |
| 2001 | 64.84 | 75.85 | 54.16 |
| 2011 | 73.0 | 80.9 | 64.6 |
(c) कुल जनसंख्या, पुरुष और महिला का प्रतिशत बंद स्तंभों में आलेखित करें $($ चित्र 3.6)।

चित्र. 3.6; भारत में साक्षरता दर, 1951-2011
संयुक्त स्तंभ आरेख
जब विभिन्न घटकों को एक ही सेट में समूहित किया जाता है या एक घटक के विभिन्न चर एक साथ रखे जाते हैं, तो उनका प्रतिनिधित्व संयुक्त स्तंभ आरेख द्वारा किया जाता है। इस विधि में, विभिन्न चरों को एक ही स्तंभ में विभिन्न आयतों के रूप में दिखाया जाता है।
उदाहरण 3.6: तालिका 3.6 में दिखाए गए आंकड़ों को दर्शाने के लिए एक संयुक्त स्तंभ आरेख बनाएं:
तालिका 3.6; भारत में बिजली की कुल उत्पत्ति (बिलियन किलोवाट घंटे में)
| वर्ष | तापीय | जलविद्युत | परमाणु | कुल |
|---|---|---|---|---|
| 2008-09 | 616.2 | 110.1 | 14.9 | 741.2 |
| $2009-10$ | 677.1 | 104.1 | 18.6 | 799.8 |
| $2010-11$ | 704.3 | 114.2 | 26.3 | 844.8 |
स्रोत: आर्थिक सर्वेक्षण, 2011-12
निर्माण
(क) आँकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करें।
(ख) एकल पट्टी दिए गए वर्ष में कुल विद्युत उत्पादन को दर्शाएगी और थर्मल, जलविद्युत तथा परमाणु विद्युत उत्पादन को पट्टी की कुल लंबाई को विभाजित करके चित्र 3.7 के अनुसार दिखाया जाएगा।
पाई आरेख
पाई आरेख आँकड़ों के निरूपण का एक अन्य आलेखीय तरीका है। इसे दिए गए गुणधर्म के कुल मान को एक वृत्त द्वारा दर्शाने के लिए बनाया जाता है। वृत्त को संगत कोणों के अनुसार विभाजित करके आँकड़ों के उपसमुच्चयों को दर्शाया जाता है। इसलिए इसे विभाजित वृत्त आरेख भी कहा जाता है।
प्रत्येक चर का कोण निम्न सूत्रों का प्रयोग करके परिकलित किया जाता है।

चित्र 3.7; भारत में सकल विद्युत उत्पादन
$\dfrac{\text{दिए गए राज्य/क्षेत्र का मान X 360}}{\text{सभी राज्यों/क्षेत्रों का कुल मान}}$
यदि आँकड़े प्रतिशत रूप में दिए गए हों, तो कोण निम्न सूत्र का प्रयोग करके परिकलित किए जाते हैं।
$\dfrac{\text{x का प्रतिशत X 360}}{100}$
उदाहरण के लिए, भारत की कुल जनसंख्या को ग्रामीण और शहरी जनसंख्या के अनुपात के साथ दिखाने के लिए एक पाई आरेख बनाया जा सकता है। इस स्थिति में, उपयुक्त त्रिज्या का एक वृत्त कुल जनसंख्या को दर्शाने के लिए खींचा जाता है और उसे ग्रामीण तथा शहरी जनसंख्या में उपविभाजित कर संगत कोणों द्वारा दर्शाया जाता है।
उदाहरण 3.7: तालिका 3.7 (a) में दिए गए आंकड़ों को एक उपयुक्त आरेख द्वारा प्रस्तुत करें।
कोणों की गणना
(a) भारतीय निर्यात के प्रतिशत को आरोही क्रम में व्यवस्थित करें।
(b) विश्व के प्रमुख क्षेत्रों/देशों को भारत के निर्यात मूल्यों को दर्शाने के लिए कोणों की डिग्री की गणना करें, तालिका 3.7 (b)। यह प्रतिशत को 3.6 के स्थिरांक से गुणा करके किया जा सकता है, जैसा कि वृत्त में कुल डिग्री की संख्या को 100 से विभाजित करके प्राप्त किया गया है, अर्थात् $360 / 100$।
तालिका 3.7 (a); 2010-11 में विश्व के प्रमुख क्षेत्रों को भारत का निर्यात
| इकाई/क्षेत्र | भारतीय निर्यात का % |
|---|---|
| यूरोप | 20.2 |
| अफ्रीका | 6.5 |
| अमेरिका | 14.8 |
| एशिया और आसियान | 56.2 |
| अन्य | 2.3 |
| कुल | 100 |
(c) वृत्त को आवश्यक विभाजनों में बाँटकर आंकड़ों को चित्रित करें ताकि विभिन्न क्षेत्रों/देशों को भारत के निर्यात के हिस्से को दिखाया जा सके (चित्र 3.8)।
तालिका 3.7 (b); 2010-11 में विश्व के प्रमुख क्षेत्रों को भारत का निर्यात
| देश | C | गणना | डिग्री |
|---|---|---|---|
| यूरोप | 20.2 | $20.2 \times 3.6 =72.72$ | $73^{\circ}$ |
| अफ्रीका | 6.5 | $6.5 \times 3.6 =23.4$ | $23^{\circ}$ |
| अमेरिका | 14.8 | $14.8 \times 3.6 =53.28$ | $53^{\circ}$ |
| एशिया और आसियान | 56.2 | $56.2 \times 3.6 =202.32$ | $203^{\circ}$ |
| अन्य | 2.3 | $2.3 \times 3.6 =8.28$ | $8^{\circ}$ |
| कुल | $\mathbf{1 0 0}$ | $\mathbf{6 6 0}^{\circ}$ |
निर्माण
(क) आरेखित किए जाने वाले वृत्त के लिए एक उपयुक्त त्रिज्या चुनें। दिए गए डेटा सेट के लिए 3, 4 या 5 $\mathrm{cm}$ की त्रिज्या चुनी जा सकती है।
(ख) वृत्त के केंद्र से चाप तक एक रेखा त्रिज्या के रूप में खींचें।
(ग) प्रत्येक वाहन श्रेणी के लिए वृत्त की चाप से कोणों को घड़ी की सुई की दिशा में आरोही क्रम में मापें, छोटे कोण से प्रारंभ करें।
(घ) शीर्षक, उप-शीर्षक और लीजेंड जोड़कर आरेख को पूर्ण करें। प्रत्येक चर/श्रेणी के लिए लीजेंड चिह्न चुना जाए और विभिन्न छायाओं/रंगों से हाइलाइट किया जाए।
सावधानियाँ
(क) वृत्त न तो इतना बड़ा हो कि स्थान में समा न सके और न ही इतना छोटा कि अपठनीय हो जाए।
(ख) बड़े कोण से प्रारंभ करने से त्रुटि का संचय होगा जिससे छोटे कोण का आरेखण कठिन हो जाएगा।

चित्र 3.8; भारतीय निर्यात की दिशा 2010-11
प्रवाह मानचित्र/चार्ट
फ्लो चार्ट ग्राफ और मानचित्र का संयोजन होता है। इसे वस्तुओं या लोगों की उत्पत्ति स्थल और गंतव्य स्थल के बीच आवाजाही दिखाने के लिए बनाया जाता है। इसे गतिशील मानचित्र भी कहा जाता है। परिवहन मानचित्र, जो यात्रियों, वाहनों आदि की संख्या दिखाता है, फ्लो चार्ट का सबसे अच्छा उदाहरण है। इन चार्ट्स को समानुपाती चौड़ाई की रेखाओं का उपयोग करके बनाया जाता है। कई सरकारी एजेंसियां विभिन्न मार्गों पर परिवहन के साधनों की घनत्व दिखाने के लिए फ्लो मानचित्र तैयार करती हैं। फ्लो मानचित्र/चार्ट आमतौर पर नीचे दिए गए दो प्रकार के डेटा को दर्शाने के लिए बनाए जाते हैं:
- वाहनों की संख्या और आवृत्ति उनकी गति की दिशा के अनुसार
- यात्रियों की संख्या और/या परिवहित वस्तुओं की मात्रा।
फ्लो मानचित्र तैयार करने की आवश्यकताएँ
(क) एक मार्ग मानचित्र जिसमें वांछित परिवहन मार्गों के साथ-साथ संयोजक स्टेशन दिखाए गए हों।
(ख) वस्तुओं, सेवाओं, वाहनों की संख्या आदि की आवाजाही से संबंधित डेटा, साथ ही आंदोलन के उत्पत्ति और गंतव्य बिंदु।
(ग) एक पैमाने का चयन जिसके माध्यम से यात्रियों और वस्तुओं की मात्रा या वाहनों की संख्या से संबंधित डेटा को दर्शाया जाएगा।
तालिका 3.8; दिल्ली और आसपास के क्षेत्रों के चयनित मार्गों की ट्रेनों की संख्या
| क्र. सं. |
रेलवे मार्ग |
ट्रेनों की संख्या |
|---|---|---|
| 1. | ओल्ड दिल्ली - न्यू दिल्ली | 50 |
| 2. | न्यू दिल्ली-निजामुद्दीन | 40 |
| 3. | निजामुद्दीन-बदरपुर | 30 |
| 4 | निजामुद्दीन-सरोजिनी नगर | 12 |
| 5. | सरोजिनी नगर - पूसा रोड | 8 |
| 6. | ओल्ड दिल्ली - सदर बाजार | 32 |
| 7. | उद्योग नगर-टिकरी कलां | 6 |
| 8. | पूसा रोड - पेहलादपुर | 15 |
| 9. | साहिबाबाद-मोहन नगर | 18 |
| 10. | ओल्ड दिल्ली - सिलमपुर | 33 |
| 11. | सिलमपुर - नंद नगरी | 12 |
| 12. | सिलमपुर-मोहन नगर | 21 |
| 13. | ओल्ड दिल्ली-शालीमार बाग | 16 |
| 14. | सदर बाजार-उद्योग नगर | 18 |
| 15. | ओल्ड दिल्ली - पूसा रोड | 22 |
| 16. | पेहलादपुर - पालम विहार | 12 |
उदाहरण 3.10: टेबल 3.8 में दी गई जानकारी के अनुसार दिल्ली और आसपास के क्षेत्रों में चलने वाली ट्रेनों की संख्या को दर्शाने के लिए एक प्रवाह मानचित्र बनाइए।
निर्माण
(a) दिल्ली और आसपास के क्षेत्रों का एक रूपरेखा मानचित्र लीजिए, जिसमें रेलवे लाइन और नोडल स्टेशन दर्शाए गए हों (चित्र 3.9)।
(b) ट्रेनों की संख्या को दर्शाने के लिए एक पैमाना चुनिए। यहां अधिकतम संख्या 50 और न्यूनतम 6 है। यदि हम $1 \mathrm{~cm}=50$ ट्रेनों का पैमाना चुनते हैं, तो अधिकतम और न्यूनतम संख्या को क्रमशः $10 \mathrm{~mm}$ और $1.2 \mathrm{~mm}$ मोटी लाइनों की पट्टी से दर्शाया जाएगा।
(c) दिए गए रेल मार्ग के बीच प्रत्येक मार्ग की पट्टी की मोटाई को चित्रित कीजिए (चित्र 3.10)।
(d) एक सोपानाकार पैमाना लीजिए और पट्टी के भीतर नोडल बिंदुओं (स्टेशनों) को दर्शाने के लिए कोई विशिष्ट चिह्न या प्रतीक चुनिए।

आकृति 3.9; दिल्ली का मानचित्र

आकृति 3.10; दिल्ली का यातायात (रेलवे) प्रवाह मानचित्र
उदाहरण 3.10: आकृति 3.11 में दिखाए गए अनुसार गंगा बेसिन का जल प्रवाह मानचित्र बनाइए।

आकृति 3.11; गंगा बेसिन
निर्माण
(a) एक पैमाना लीजिए जिसमें $1 \mathrm{~cm}$ चौड़ाई की पट्टी = 50,000 क्यूसेक पानी हो।
(b) आकृति 3.12 में दिखाए गए अनुसार आरेख बनाइए।

आकृति 3.12; प्रवाह मानचित्र का निर्माण
थीमेटिक मानचित्र
ग्राफ और आरेख डेटा के विभिन्न लक्षणों के भीतर आंतरिक विचरणों की तुलना प्रस्तुत करने में उपयोगी उद्देश्य की पूर्ति करते हैं। तथापि, ग्राफों और आरेखों के प्रयोग से कभी-कभी क्षेत्रीय दृष्टिकोण उत्पन्न नहीं होता। इसलिए, क्षेत्रीय बंटनों के प्रतिरूपों या अंतरिक्ष पर विचरणों के लक्षणों को समझने के लिए विविध प्रकार के मानचित्र भी बनाए जा सकते हैं। इन मानचित्रों को बंटन मानचित्र भी कहा जाता है।
एक थीमेटिक मानचित्र बनाने की आवश्यकताएँ
(क) चयनित थीम के बारे में राज्य/ज़िला स्तर का डेटा।
(ख) अध्ययन क्षेत्र का रूपरेखा मानचित्र जिसमें प्रशासनिक सीमाएँ हों।
(ग) क्षेत्र का भौतिक मानचित्र। उदाहरण के लिए, जनसंख्या बंटन के लिए भौतिकी मानचित्र और परिवहन मानचित्र बनाने के लिए राहत और अपवाह मानचित्र।
थीमेटिक मानचित्र बनाने के नियम
(i) थीमेटिक मानचित्रों का चित्रांकन सावधानीपूर्वक योजनाबद्ध किया जाना चाहिए। अंतिम मानचित्र निम्नलिखित घटकों को उचित रूप से दर्शाना चाहिए:
क. क्षेत्र का नाम
ख. विषय-वस्तु का शीर्षक
ग. डेटा का स्रोत और वर्ष
घ. प्रतीकों, चिह्नों, रंगों, छायाओं आदि का संकेत
ङ. पैमाना
(ii) थीमेटिक मानचित्रण के लिए प्रयुक्त होने वाली उपयुक्त विधि का चयन।
निर्माण विधि के आधार पर थीमेटिक मानचित्रों का वर्गीकरण
विषय-सम्बन्धी मानचित्रों को, सामान्यतः, मात्रात्मक और गैर-मात्रात्मक मानचित्रों में वर्गीकृत किया जाता है। मात्रात्मक मानचित्र आँकड़ों के भीतर विभिन्नताओं को दर्शाने के लिए बनाए जाते हैं। उदाहरण के लिए, वे मानचित्र जो $200 \mathrm{~cm}$ से अधिक, $100$ से $200 \mathrm{~cm}$, $50$ से $100 \mathrm{~cm}$ और $50 \mathrm{~cm}$ से कम वर्षा प्राप्त करने वाले क्षेत्रों को दर्शाते हैं, मात्रात्मक मानचित्र कहलाते हैं। इन मानचित्रों को सांख्यिकीय मानचित्र भी कहा जाता है। दूसरी ओर, गैर-मात्रात्मक मानचित्र दी गई सूचना के वितरण में अमापीय विशेषताओं को दर्शाते हैं, जैसे कि उच्च और निम्न वर्षा प्राप्त करने वाले क्षेत्रों को दिखाने वाला मानचित्र। इन मानचित्रों को गुणात्मक मानचित्र भी कहा जाता है। समय की सीमा के अंतर्गत इन विभिन्न प्रकार के विषय-सम्बन्धी मानचित्रों को बनाने की चर्चा करना सम्भव नहीं होगा। इसलिए, हम निम्नलिखित प्रकार के मात्रात्मक मानचित्रों की रचना की विधियों तक सीमित रहेंगे:
(a) डॉट मानचित्र
(b) कोरोप्लेथ मानचित्र
(c) आइसोप्लेथ मानचित्र
डॉट मानचित्र
डॉट मानचित्र जनसंख्या, पशु, फसलों के प्रकार आदि जैसी घटनाओं के वितरण को दर्शाने के लिए बनाए जाते हैं। चुनी गई मापदण्ड के अनुसार समान आकार के बिन्दुओं को दिए गए प्रशासनिक इकाइयों पर चिह्नित किया जाता है ताकि वितरण के प्रतिरूपों को उजागर किया जा सके।
आवश्यकता
(a) दिए गए क्षेत्र का एक प्रशासनिक मानचित्र जो राज्य/जिला/प्रखण्ड की सीमाएँ दर्शाता हो। (b) चुनी गई प्रशासनिक इकाइयों के लिए चुने गए विषय पर सांख्यिकीय आँकड़े, अर्थात् कुल जनसंख्या, पशु आदि।
(c) एक बिन्दु के मान को निर्धारित करने के लिए मापदण्ड का चयन।
(डी) क्षेत्र का भौतिक भूगोल मानचित्र, विशेष रूप से राहत और जल निकासी मानचित्र।
सावधानी
(क) विभिन्न प्रशासनिक इकाइयों की सीमाओं को दर्शाने वाली रेखाएँ बहो मोटी और गाढ़ी नहीं होनी चाहिए।
(ख) सभी बिंदु एक ही आकार के होने चाहिए।
उदाहरण 3.12: तालिका 3.9 में दिए गए 2001 की जनसंख्या आंकड़ों को दर्शाने के लिए एक बिंदु मानचित्र बनाइए।
तालिका 3.9; भारत की जनसंख्या, 2001
| क्र. सं. |
राज्य/केंद्र शासित प्रदेश |
कुल जनसंख्या | बिंदुओं की संख्या |
|---|---|---|---|
| 1. | जम्मू और कश्मीर | 10,069,917 | 100 |
| 2. | हिमाचल प्रदेश | 6,077,248 | 60 |
| 3. | पंजाब | 24,289,296 | 243 |
| 5. | उत्तराखंड | 8,479,562 | 85 |
| 6. | हरियाणा | 21,082,989 | 211 |
| 7. | दिल्ली | 13,782,976 | 138 |
| 8. | राजस्थान | 56,473,122 | 565 |
| 9. | उत्तर प्रदेश | 166,052,859 | 1,660 |
| 10. | बिहार | 82,878,796 | 829 |
| 11. | सिक्किम | 540,493 | 5 |
| 12. | अरुणाचल प्रदेश | 1,091,117 | 11 |
| 13. | नागालैंड | 1,988,636 | 20 |
| 14. | मणिपुर | 2,388,634 | 24 |
| 15. | मिजोरम | 891,058 | 89 |
| 16. | त्रिपुरा | 3,191,168 | 32 |
| 17. | मेघालय | 2,306,069 | 23 |
| 18. | असम | 26,638,407 | 266 |
| 19. | पश्चिम बंगाल | 80,221,171 | 802 |
| 20. | झारखंड | 26,909,428 | 269 |
| 21. | ओडिशा | 36,706,920 | 367 |
| 22. | छत्तीसगढ़ | 20,795,956 | 208 |
| 23. | मध्य प्रदेश | 60,385,118 | 604 |
| 24. | गुजरात | 50,596,992 | 506 |
| 25. | महाराष्ट्र | 96,752,247 | 968 |
| 26. | आंध्र प्रदेश | 75,727,541 | 757 |
| 27. | कर्नाटक | 52,733,958 | 527 |
| 28. | गोवा | 1,343,998 | 13 |
| 29. | केरल | 31,838,619 | 318 |
| 30. | तमिलनाडु | 62,110,839 | 621 |
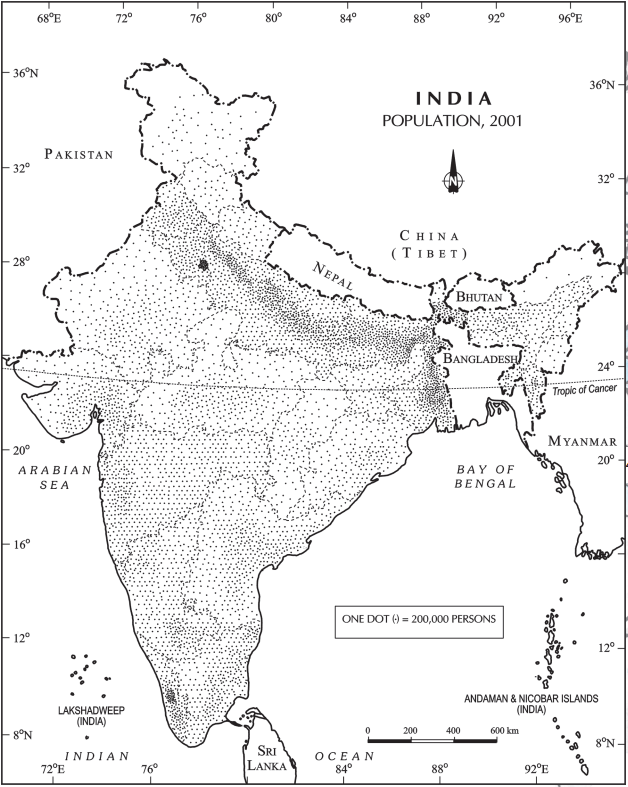
निर्माण
(a) बिंदु का आकार और मान चुनें।
(b) दिए गए स्केल का उपयोग करके प्रत्येक राज्य में बिंदुओं की संख्या निर्धारित करें। उदाहरण के लिए, महाराष्ट्र में बिंदुओं की संख्या होगी 9,67,52,247 /100,000 =967.52। इसे 968 के रूप में पूर्णांकित किया जा सकता है, क्योंकि भिन्नात्मक मान 0.5 से अधिक है।
(c) सभी राज्यों में निर्धारित संख्या के अनुसार प्रत्येक राज्य में बिंदुओं को रखें।
(d) भारत के भौतिक/राहत मानचित्र का परामर्श लें ताकि पहाड़ी, रेगिस्तान और/या हिमाच्छादित क्षेत्रों की पहचान की जा सके और ऐसे क्षेत्रों में कम संख्या में बिंदुओं को चिह्नित करें।
कोरोप्लेथ मानचित्र
कोरोप्लेथ मानचित्र भी आंकड़ों की विशेषताओं को दर्शाने के लिए बनाए जाते हैं क्योंकि वे प्रशासनिक इकाइयों से संबंधित होते हैं। इन मानचित्रों का उपयोग जनसंख्या घनत्व, साक्षरता/वृद्धि दर, लिंग अनुपात आदि को दर्शाने के लिए किया जाता है।
कोरोप्लेथ मानचित्र बनाने की आवश्यकता
(a) क्षेत्र का एक मानचित्र जो विभिन्न प्रशासनिक इकाइयों को दर्शाता हो।
(b) प्रशासनिक इकाइयों के अनुसार उपयुक्त सांख्यिकीय आंकड़े।
अनुसरण करने योग्य चरण
(a) आंकड़ों को आरोही या अवरोही क्रम में व्यवस्थित करें।
(b) आंकड़ों को 5 श्रेणियों में समूहित करें ताकि बहुत अधिक, अधिक, मध्यम, कम और बहुत कम सांद्रता को दर्शाया जा सके।
(c) श्रेणियों के बीच अंतराल को निम्नलिखित सूत्र पर पहचाना जा सकता है अर्थात्, परास/5 और परास = अधिकतम मान - न्यूनतम मान।
(d) चयनित श्रेणियों को दर्शाने के लिए प्रयोग किए जाने वाले पैटर्न, छायांकन या रंग को बढ़ते या घटते क्रम में चिह्नित किया जाना चाहिए।
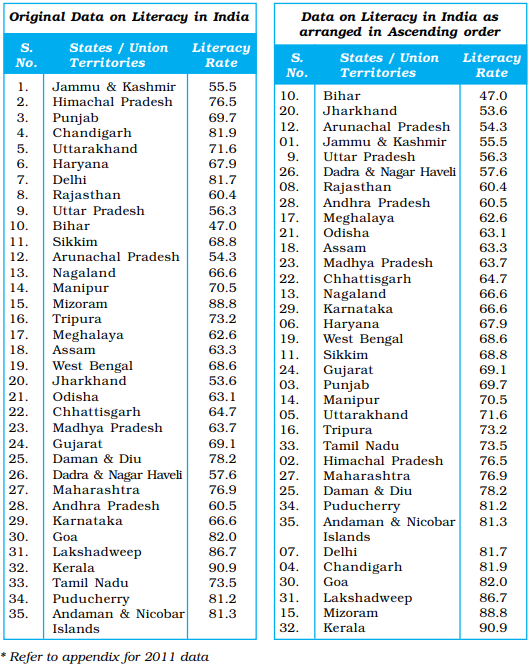
उदाहरण 3.13: तालिका 3.10 में दिए गए अनुसार 2001 में भारत में साक्षरता दरों को दर्शाने के लिए एक कोरोप्लेथ मानचित्र का निर्माण करें।
निर्माण
(क) आँकड़ों को ऊपर दिखाए अनुसार आरोही क्रम में व्यवस्थित करें।
(ख) आँकड़ों के भीतर परास (range) की पहचान करें। वर्तमान स्थिति में, सबसे कम और सबसे अधिक साक्षरता दर दर्ज करने वाले राज्य बिहार (47 %) और केरल (90.9 %) हैं। इसलिए, परास होगी 91.0 – 47.0 = 44.0
(ग) परास को 5 से विभाजित करके बहुत कम से लेकर बहुत अधिक तक श्रेणियाँ प्राप्त करें। (44.0) ÷ 5 = 8.80। हम इस मान को निकटतम पूर्ण संख्या में बदल सकते हैं, अर्थात् 9.0
(घ) श्रेणियों की संख्या और प्रत्येक श्रेणी की परास निर्धारित करें। सबसे न्यूनतम मान 47.0 में 9.0 जोड़ते जाएँ। अंततः हमें निम्नलिखित श्रेणियाँ प्राप्त होंगी:
47–56 बहुत कम (बिहार, झारखंड, अरुणाचल प्रदेश, जम्मू-कश्मीर)
56–65 कम (उत्तर प्रदेश, राजस्थान, आंध्र प्रदेश, मेघालय, ओडिशा, असम, मध्य प्रदेश, छत्तीसगढ़)
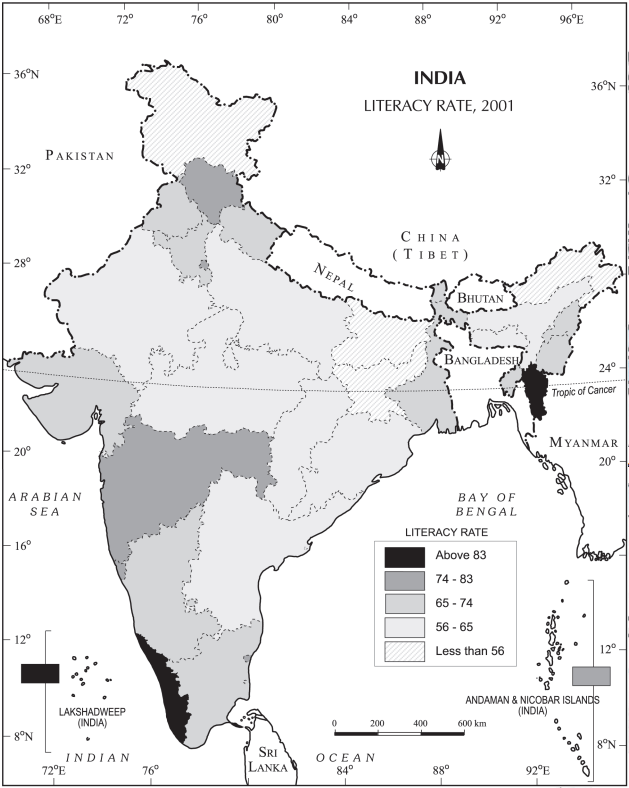
Fig. 3.14; साक्षरता दर, 2001
Table 3.10; भारत में साक्षरता दर, 2001
65–74 मध्यम (नागालैंड, कर्नाटक, हरियाणा, पश्चिम बंगाल, सिक्किम, गुजरात, पंजाब, मणिपुर, उत्तराखंड, त्रिपुरा, तमिलनाडु)
74–83 उच्च (हिमाचल प्रदेश, महाराष्ट्र, दिल्ली, गोवा)
83–92 बहुत उच्च (मिजोरम, केरल)
(e) प्रत्ये श्रेणी को निम्न से उच्च रंगों तक छायाओं/पैटर्न आवंटित करें।
(f) चित्र 3.14 के अनुसार मानचित्र तैयार करें।
(g) मानचित्र डिज़ाइन के गुणधर्मों के अनुसार मानचित्र को पूर्ण करें।
समबारी मानचित्र
हमने देखा है कि प्रशासनिक इकाइयों से सम्बद्ध आँकड़े कोरोप्लेथ मानचित्रों द्वारा दर्शाए जाते हैं। तथापि, कई स्थितियों में आँकड़ों के भीतर विचरण प्राकृतिक सीमाओं के आधार पर भी देखे जा सकते हैं। उदाहरणस्वरूप, ढलान की सीढ़ियों, तापमान, वर्षा की घटना आदि में निरंतरता के गुण होते हैं। इन भौगोलिक तथ्यों को मानचित्र पर समान मानों की रेखाएँ खींचकर दर्शाया जा सकता है। ऐसे सभी मानचित्र समबारी मानचित्र कहलाते हैं। समबारी शब्द ‘आइसो’ जिसका अर्थ समान है और ‘प्लेथ’ जिसका अर्थ रेखाएँ हैं, से बना है। इस प्रकार, एक काल्पनिक रेखा जो समान मानों के स्थानों को जोड़ती है, समबारी कहलाती है। अधिकतर खींची जाने वाली समबारियों में आइसोथर्म (समान तापमान), आइसोबार (समान दबाव), आइसोहाइट (समान वर्षा), आइसोनेफ (समान बादलों की मात्रा), आइसोहेल (समान धूप), कन्टूर (समान ऊँचाई), आइसोबाथ (समान गहराई), आइसोहैलीन (समान लवणता) आदि सम्मिलित हैं।
आवश्यकता
(a) विभिन्न स्थानों के बिंदु स्थान दर्शाने वाला आधार रेखा मानचित्र।
(b) निश्चित समयावधि के दौरान तापमान, दबाव, वर्षा आदि का उपयुक्त आँकड़ा।
(c) फ्रेंच कर्व आदि विशेष रूप से ड्राइंग उपकरण।
पालन करने योग्य नियम
(a) मानों का समान अंतराल चुना जाए।
(b) 5, 10 या 20 का अंतराल आदर्श माना जाता है।
(c) आइसोप्लेथ का मान रेखा के किसी एक ओर या बीच में रेखा को तोड़कर लिखा जाना चाहिए।
इंटरपोलेशन
इंटरपोलेशन का उपयोग दो स्टेशनों/स्थानों पर दर्ज किए गए मानों के बीच मध्यवर्ती मानों को सम्मिलित करने के लिए किया जाता है, जैसे कि चेन्नई और हैदराबाद में दर्ज तापमान या दो बिंदुओं के स्पॉट ऊँचाइयाँ। सामान्यतः, समान मान वाले स्थानों को जोड़ने वाली आइसोप्लेथ बनाना भी इंटरपोलेशन कहलाता है।
इंटरपोलेशन की विधि
इंटरपोलेशन के लिए निम्नलिखित चरणों का पालन करें:
(a) सर्वप्रथम, मानचित्र पर दिए गए न्यूनतम और अधिकतम मानों को निर्धारित करें।
(b) मानों की सीमा की गणना करें अर्थात् सीमा $=$ अधिकतम मान - न्यूनतम मान।
(c) सीमा के आधार पर, अंतराल को 5, 10, 15 आदि जैसे पूर्णांक में निर्धारित करें।
आइसोप्लेथ बनाने का सटीक बिंदु निम्नलिखित सूत्रों का उपयोग करके निर्धारित किया जाता है।
$\dfrac{\text{दो बिंदुओं के बीच की दूरी सेंटीमीटर में}}{\text{संगत बिंदुओं के दो मानों के बीच का अंतर}}\times\text{आंतरिक अंतर}$
अंतराल वास्तविक मान और इंटरपोलेटेड मान के बीच का अंतर होता है। उदाहरण के लिए, दो स्थानों के आइसोथर्म मानचित्र में $28^{\circ}\mathrm{C}$ और $33^{\circ}\mathrm{C}$ दर्शाए गए हैं और आप $30^{\circ}\mathrm{C}$ आइसोथर्म खींचना चाहते हैं, तो दोनों बिंदुओं के बीच की दूरी मापें। मान लीजिए, दूरी $1 \mathrm{~cm}$ या $10 \mathrm{~mm}$ है और 28 तथा 33 के बीच का अंतर 5 है, जबकि 30, 28 से 2 अंक दूर है और 33 से 3 अंक पीछे है, इस प्रकार 30 का सटीक बिंदु होगा
इस प्रकार, $30^{\circ}\mathrm{C}$ की समतापीय रेखा को $28^{\circ}\mathrm{C}$ से $4 \mathrm{~mm}$ दूर या $33^{\circ}\mathrm{C}$ से $6 \mathrm{~mm}$ आगे रखकर खींचा जाएगा।
(घ) सबसे पहले न्यूनतम मान की समबंधीय रेखाएँ खींचें; अन्य समबंधीय रेखाएँ तदनुसार खींची जा सकती हैं।

आकृति $3.15:$ समबंधीय रेखाओं का चित्रण
अभ्यास
1. नीचे दिए गए चार विकल्पों में से सही उत्तर चुनें:
(i) निम्नलिखित में से कौन-सा मानचित्र जनसंख्या वितरण दिखाता है:
(क) कोरोप्लेथ मानचित्र
(ख) समबंधीय मानचित्र
(ग) बिंदु मानचित्र
(घ) वर्गमूल मानचित्र
(ii) निम्नलिखित में से कौन-सा जनसंख्या की दशकीय वृद्धि को दर्शाने के लिए सर्वाधिक उपयुक्त है?
(क) रेखा ग्राफ
(ख) दंड आरेख
(ग) वृत्त आरेख
(घ) प्रवाह आरेख
(iii) बहुग्राफ का निर्माण किसे दर्शाने के लिए किया जाता है:
(क) केवल एक चर
(ख) केवल दो चर
(ग) दो से अधिक चर
(घ) उपर्युक्त में से कोई नहीं
(iv) निम्नलिखित में से कौन-सा मानचित्र “गतिशील मानचित्र” के रूप में जाना जाता है?
(क) बिंदु मानचित्र
(ख) कोरोप्लेथ
(ग) समबंधीय
(घ) प्रवाह मानचित्र
2. निम्नलिखित प्रश्नों के उत्तर लगभग 30 शब्दों में दीजिए:
(i) थीमैटिक मानचित्र क्या है?
(ii) बहु-बार आरेख और संयुक्त बार आरेख के बीच अंतर बताइए।
(iii) डॉट मानचित्र बनाने के लिए क्या आवश्यकताएँ होती हैं?
(iv) ट्रैफिक फ्लो मानचित्र बनाने की विधि का वर्णन कीजिए।
(v) आइसोप्लेथ मानचित्र क्या है? इंटरपोलेशन कैसे किया जाता है?
(vi) कोरोप्लेथ मानचित्र तैयार करने के लिए अनुसरण किए जाने वाले महत्वपूर्ण चरणों का वर्णन और चित्रण कीजिए।
(vii) पाई-आरेख की सहायता से आँकड़ों को निरूपित करने के महत्वपूर्ण चरणों की चर्चा कीजिए।
गतिविधि
1. निम्नलिखित आँकड़ों को उपयुक्त आरेख की सहायता से निरूपित कीजिए।
भारत: शहरीकरण के रुझान 1901-2001
| वर्ष | दशकीय वृद्धि (%) |
|---|---|
| 1911 | 0.35 |
| 1921 | 8.27 |
| 1931 | 19.12 |
| 1941 | 31.97 |
| 1951 | 41.42 |
| 1961 | 26.41 |
| 1971 | 38.23 |
| 1981 | 46.14 |
| 1991 | 36.47 |
| 2001 | 31.13 |
2. निम्नलिखित आँकड़ों को उपयुक्त आरेख की सहायता से निरूपित कीजिए।
भारत: प्राथमिक और उच्च प्राथमिक विद्यालयों में साक्षरता और नामांकन अनुपात
| वर्ष | साक्षरता अनुपात | नामांकन अनुपात प्राथमिक |
नामांकन अनुपात उच्च प्राथमिक |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|
| व्यक्ति | पुरुष | महिला | लड़के | लड़कियाँ | कुल | लड़के | लड़कियाँ | कुल | ||
| $1950-51$ | 18.3 | 27.2 | 8.86 | 60.6 | 25 | 42.6 | 20.6 | 4.6 | 12.7 | |
| $1999-2000$ | 65.4 | 75.8 | 54.2 | 104 | 85 | 94.9 | 67.2 | 50 | 58.8 |
3. निम्नलिखित आँकड़ों को पाई-आरेख की सहायता से निरूपित कीजिए।
भारत: भूमि उपयोग 1951-2001
| 1950-51 | 1998-2001 | |
|---|---|---|
| निवाई क्षेत्र | 42 | 46 |
| वन | 14 | 22 |
| खेती के लिए उपलब्ध नहीं | 17 | 14 |
| परती भूमि | 10 | 8 |
| चरागाह और वृक्ष | 9 | 5 |
| सांस्कृतिक अपशिष्ट भूमि | 8 | 5 |
4. नीचे दी गई तालिका का अध्ययन करें और दिए गए आरेख/नक्शे बनाएं।
प्रमुख राज्यों में चावल का क्षेत्रफल और उत्पादन
| राज्य | क्षेत्रफल हज़ार हेक्टेयर |
कुल क्षेत्रफल में % |
उत्पादन हज़ार टन |
कुल उत्पादन में % |
|---|---|---|---|---|
| पश्चिम बंगाल | 5,435 | 12.3 | 12,428 | 14.6 |
| उत्तर प्रदेश | 5,839 | 13.2 | 11,540 | 13.6 |
| आंध्र प्रदेश | 4,028 | 9.1 | 12,428 | 13.5 |
| पंजाब | 2,611 | 5.9 | 9,154 | 10.8 |
| तमिलनाडु | 2,113 | 4.8 | 7,218 | 8.5 |
| बिहार | 3,671 | 8.3 | 5,417 | 6.4 |
(a) प्रत्येक राज्य में चावल के अंतर्गत क्षेत्रफल को दर्शाने के लिए एक बहु-बार आरेख बनाएं।
(b) प्रत्येक राज्य में चावल के अंतर्गत क्षेत्रफल के प्रतिशत को दर्शाने के लिए एक पाई-आरेख बनाएं।
(c) प्रत्येक राज्य में चावल के उत्पादन को दर्शाने के लिए एक डॉट नक्शा बनाएं।
(d) राज्यों में चावल के उत्पादन के प्रतिशत को दर्शाने के लिए एक कोरोप्लेथ नक्शा बनाएं।
5. कोलकाता के तापमान और वर्षा के निम्नलिखित आंकड़ों को एक उपयुक्त आरेख द्वारा दिखाएं।
| महीने | तापमान ${ }^{2}$ C में | वर्षा सेंटीमीटर में |
|---|---|---|
| जन. | 19.6 | 1.2 |
| फर. | 22.0 | 2.8 |
| मार्च | 27.1 | 3.4 |
| अप्रैल | 30.1 | 5.1 |
| मई | 30.4 | 13.4 |
| जून | 29.9 | 29.0 |
| जुलाई | 28.9 | 33.1 |
| अग. | 28.7 | 33.4 |
| सित. | 28.9 | 25.3 |
| अक्टू. | 27.6 | 12.7 |
| नव. | 23.4 | 2.7 |
| दिस. | 19.7 | 0.4 |



